原神1.1元素附着时间与反应机制详解[多图]

原神元素反应是游戏中的一个特色玩法，1.1版本元素量和附着时间如何计算？下面来看看原神1.1元素附着时间与反应机制详解

一、元素量与附着时间

元素的附着时间与元素量是互相关联、密不可分的两个数值，单独抛开一个去谈另一个是没有什么意义的。它们的关系就像函数中的两个变量的关系，存在某个对应公式，输入其一的值，就可以输出另一的值。

1.1 元素量与消耗量

同元素叠加可以理解为元素量与时间的覆盖，元素反应与破盾则是元素量被消耗而产生对应效果。元素反应与破盾存在着元素量的消耗，消耗量即为反应或破盾时剩余的元素量，消耗量也受元素间的克制影响。强度不同的元素所对应的最长持续时间与最大元素量都不同，最大元素量为在元素刚附着时的元素量，具体数据详见元素附着时间。

数据采用“最长时间-最大元素量”的格式表示，假设水火冰雷中最弱的元素具有的最大元素量为1(下同)，那么有如下的对应关系：

弱元素：9.5s-1 中元素：12s-2 强元素：16.8s-4

风和岩元素不具有自己单独的元素量与持续时间，但是存在消耗被反应元素的消耗量。风元素还额外具有扩散出去的元素(称为扩散元素)所对应的最长持续时间与元素量的独特衡量维度。弱/强风和岩即为[元素附着时间]中提到的6s/9.5s风和岩。

数据表示消耗量，有如下对应关系：

弱风/岩：0.5 强风/岩：1

对于风元素，以“最长时间-最大元素量”的格式表示扩散元素的最长时间与最大元素量，有如下的对应关系

弱风：10.7s-1.5 强风：14s-2.75

1.2 元素量的衰减模型

元素量会随附着时间的增加而衰减，附着时间为0时元素量为最大值，附着时间为最长持续时间时元素量为0。附着时间-元素量所对应的衰减模型共有两种，一为线性，二为分段(分段模型如何测出详见破盾部分)，其中主要以分段衰减为主。贴中暂不展示16.8s强元素的图像，目前仅有北斗Q的第一段爆炸附着为强元素，其余均为弱、中元素。

线性衰减模型：

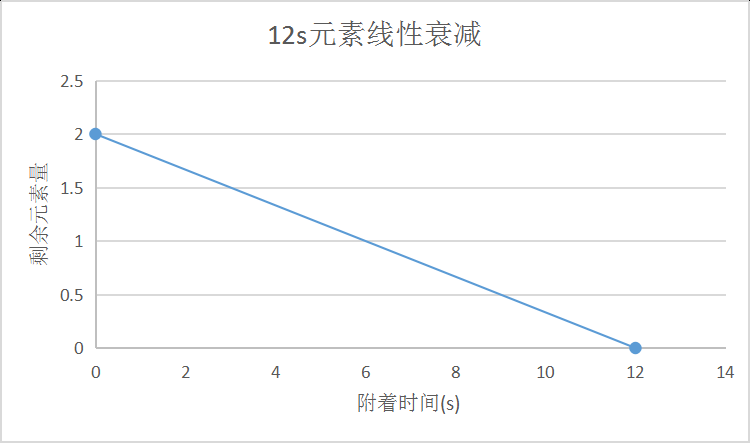
分段衰减模型(先以某方式快速衰减，后面则按线性衰减)：

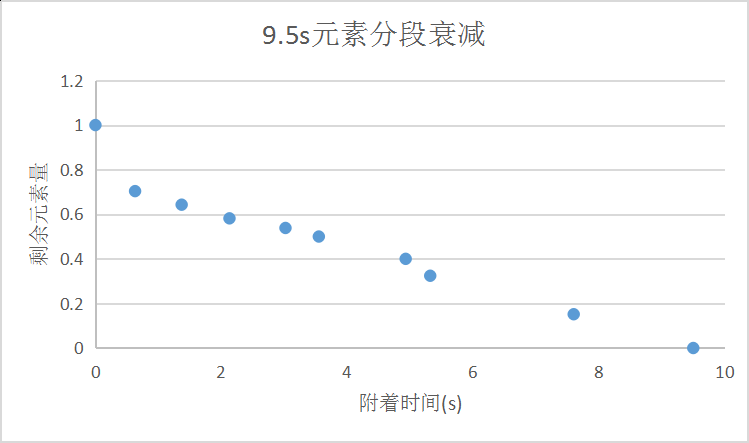
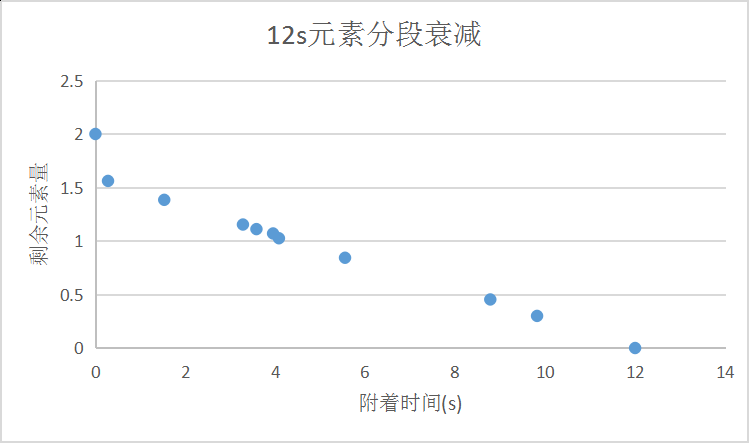
1.3 元素的主次

元素反应与叠加中的元素有主次之分，第一个附着的元素即为主元素，后续元素均为次元素(感电反应除外，会在第三部分元素反应中提到)。

在同元素叠加中，时间标准会以主元素的标准进行判定，后续的元素均为次元素仅负责补充时间与元素量而不会改变时间标准。

在元素反应中，只有主元素会残留，后续的次元素只扮演消耗主元素元素量的角色。即便次元素的元素量多于主元素的剩余元素量，次元素也不会残留。

二、同元素叠加

2.1 叠加机制理论

同元素叠加可理解为是时间的覆盖。自A元素附着过去了一段时间后又上了B元素，如果A元素的剩余时间大于B元素的补充时间，那么仍然按A元素的元素量与剩余时间计算;如果A元素的剩余时间小于B元素的补充时间，那么此元素的剩余元素量会变为B元素的元素量而剩余时间变为B元素的补充时间，可以理解为时间长的会盖住时间短的。注意，叠加中对比的不是剩余元素量的多少，而是只看谁的时间长，具体原因会在补充部分中提到。

2.2 用词解释

剩余时间：顾名思义，剩余时间为某元素在附着一定时间后无干扰情况下还可存在的时间。例如A元素为12s元素，在附着了7s后被叠加，那么剩余时间即为12s-7s=5s

时间标准：可以理解为元素的“某种密度”。例如对于9.5s元素来说，它的时间标准就是每有x的元素量，就有9.5s的持续时间。所以如果在9.5s的时间标准下有1.5的元素量，那么表现为元素会持续9.5sx1.5=14.25s。同理，如果在12s的时间标准下有1的元素量，那么表现为元素会持续12sx0.5=6s。时间标准包括也扩散元素的10.7s-1.5和14s-2.75这两个标准。

补充时间：B对A的补充时间，即为在A的时间标准下以B的元素量计算，以此算出的时间即为B对A的补充时间。例如12s元素对9.5s元素的补充时间为19s。

2.3 两个例子

? 例子 ...

例1.9.5+12+9.5的叠加

此情况下第一个9.5s元素为主元素，时间标准即为9.5s-1。12s元素叠加时对9.5s-1标准的补充时间为19s，所以必定覆盖之前的时间，同时元素量变为2。之后又叠加9.5s元素，其对于9.5s-1标准的补充时间为9.5s。所以在先前的19s的剩余时间大于9.5s时，第二次叠加的9.5s元素不会对剩余时间产生任何影响。而如果先前的19s的剩余时间小于9.5s，第二次叠加的9.5s元素会覆盖剩余时间，并重新刷新为补充时间的9.5s，满足[元素附着时间叠加机制]中该情况的分段公式。

例2.弱风扩散+9.5的叠加

此情况下弱风扩散元素为主元素，时间标准即为10.7s-1.5。9.5s元素对该标准的补充时间为10.7*2/3≈7.13s。所以当扩散元素剩余时间大于7.13s时，此叠加无影响。当扩散元素剩余时间小于7.13s时，9.5s的叠加会覆盖剩余时间并刷新元素量。此预测能与实际数据很好的符合，误差较小在接受范围内。

这里给出几组数据：1. 1.35 10.73;2. 4.35 11.60;3. 6.08 13.10;4. 8.75 15.93;5. 2.88 10.70(第一个数据代表叠加时主元素已经附着的时间，第二个数据为元素彻底消失的时间)

三、元素反应

3.1 元素反应机制理论

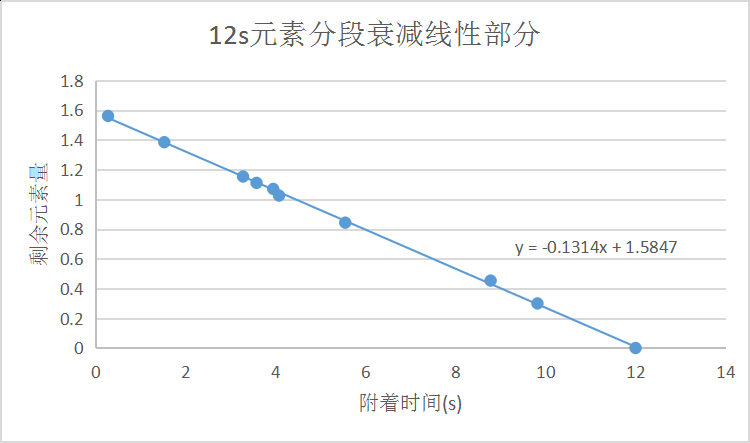
元素反应中次元素会消耗主元素的元素量，如果反应后主元素的剩余元素量不为0则会继续残留至消耗完毕。元素反应中次元素的消耗量即为最大元素量，元素存在克制情况会对应的将消耗量翻倍或减半，风和岩则直接消耗其对应的消耗量，而主元素的剩余元素量按照分段衰减模型计算。实际计算中只用得上分段模型的线性部分，单独附上对应的图像以及拟合公式。(感电反应特殊，会单独解释)

3.2 分段模型的线性部分

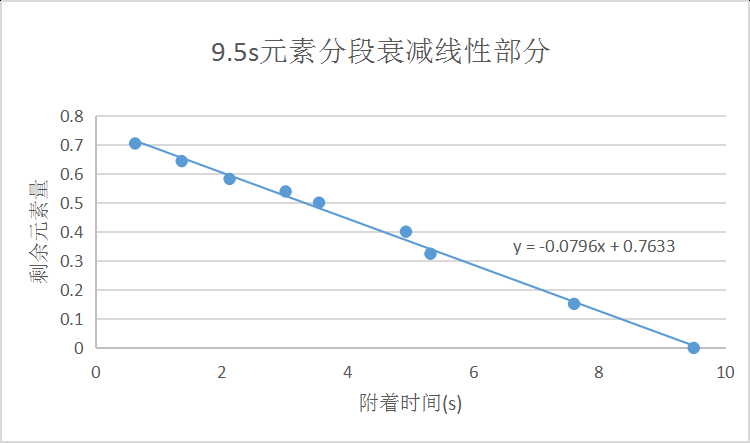
3.3 增幅反应、剧变反应与结晶反应(不含感电反应)

结合上述理论与[元素反应中的元素残留机制]中的数据简单举几个例子便于大家理解。冻结与破冰较为特别但仍符合上述规律，可详见[元素反应中的元素残留机制]中的破冰介绍。

? 例子 ...

例1.超导反应中12+9.5的反应

此情况下，12s元素为主元素，9.5s元素为次元素，反应时9.5s元素会消耗掉主元素1的元素量。为判断主元素的剩余元素量与消耗量的大小，需找到主元素衰减至1时的时间点。令上述公式y=-0.1314x+1.5847=1，求得x≈4.45s，实际测试数据为4.5s-4.6s，在误差允许范围内。所以此情况下，附着时间在约4.6s前反应会残留主元素(需要注意，在约0.9s的反应结算时间内看不出残留)，4.6s后反应则不残留元素。可认为反应消耗是令原图像向下平移对应消耗量的单位，从图像最右侧开始影响而不影响正在进行的左半端，所以残留情况下元素会残留至约4.6s

例2.融化反应中12+9.5的反应

12s元素为主元素，9.5s元素为次元素，由于火克冰，所以冰消耗火的元素量减半，火消耗冰的元素量翻倍。所以此情况只有先火后冰才可能残留火元素，而冰火顺序冰元素不会残留。9.5s的冰消耗12s火的消耗量为1的一半，即0.5。令0.5=-0.1314x+1.5847，求得x≈8.25s，实际测试数据为8.3s-8.4s，在误差允许范围内，符合实际数据。

例3.结晶反应中9.5s元素+弱岩的反应

弱岩的元素消耗量为0.5，而9.5s元素对应的分段衰减模型的线性部分为y=-0.0796x+0.7633，所以令0.5=-0.0796x+0.7633，求得x≈3.31s，实际测试数据为约3.5s，在误差允许范围内，符合实际数据。

3.4 感电反应

感电反应结算机制：两元素地位平等，每次结算同时减掉两元素各0.5的元素量，每进行一次结算造成一次感电伤害，直到有一元素被消耗完。最终残留的元素按线性衰减计算，不残留元素按分段衰减计算，两元素均不残留时沿用之前的分段点。(似乎存在如果两元素附着时间相隔过近，会导致前一元素会被少消耗一轮0.5但伤害正常触发的问题。感电还存在有时消耗一轮元素量后不造成此轮感电伤害的问题，此问题通常发生在中间轮次)

需要注意，在1.1版本更新后，雷水顺序残留机制变为与水雷顺序一致。按照上述机制，并非一次感电只会触发两次伤害，目前理论上存在一次感电五次伤害的可能，个人只试出了四次的情况。

? 例子 ...

例1.9.5+9.5的两种情况

A.当前一元素的元素量尚未衰减至0.5时，两元素的元素量都支持结算两次，此时会跳两次感电伤害而两元素均不残留。

B.当前一元素的元素量衰减至低于0.5时，前一元素只支持进行一次结算而只造成一次感电伤害，衰减至0.5的时间因其不残留所以按分段模型，为约3.5s。后一元素在一次结算后被消耗0.5的元素量，由于其为残留元素，衰减模型按线性，故会残留约4.75s。注意，后一元素应从刚开始附着时开始计算时间，而非反应结算后。

例2.12+9.5的三种情况

A.12s元素的元素量未衰减至1时，12s元素残留而9.5s元素不残留，跳两次感电伤害。12s元素残留按线性模型，被消耗1的元素量后会残留至约6s。

B.12s元素的元素量衰减至低于1但不低于0.5时，会跳两次感电伤害而两元素均不残留，由于均不残留，12s元素沿用之前6s的分段点。

C.12s元素的元素量未衰减至低于0.5时，会跳一次感电伤害而后一元素残留。12s元素由于不残留按分段模型，衰减至0.5的点为约8.3s。而后一元素由于残留按线性模型，在被消耗0.5的元素量后，会残留约4.75s。

3.5 扩散反应

风元素消耗被扩散元素的元素量情况与上面的结晶反应相同([扩散无法正常触发]中提到的扩散问题可能是目前只有在被扩散元素的元素量大于0.5时才可反应，但不清楚为什么强风对于此时间的要求会更苛刻，弱风对应的时间正好对应公式算出的分段点)，单纯的扩散元素与其他元素叠加或反应的情况不再赘述，与上述正常反应相同。此条着重讲一下扩散元素元素量的问题。

强风扩散会消耗1的元素量，但当被扩散元素的剩余元素量小于1却仍大于可反应界限时，扩散出去的元素量会随之减少，变化类似于元素衰减分段情况。但此情况下被扩散元素是12s元素和9.5s元素的对应情况不同，9.5s元素的会衰减的比12s元素更快，具体原因不得而知。

弱风由于最大消耗量即为0.5与上面提到的可发生扩散反应的临界点相同，故而不存在上述情况。

(此条内容比较复杂，暂不展开叙述)

四、关于破盾/甲

本条不涉及具体破盾/甲数据等指导，只简单介绍破盾/甲在元素量层面的根本机制，以及如何通过破盾/甲得出上述分段衰减结论。

4.1 破盾/甲

原神内针对例如法师无敌盾和愚人众减伤甲，破盾值采取的是元素量消耗+伤害的综合计算，消耗量会受单独设置系数与元素相克影响。减伤甲免疫所有伤害只按元素消耗量进行(岩甲和冰甲破冰除外)，所以下述测试在避免破冰影响下对骗骗花的冰甲进行，破盾/甲的详细内容会在以后提及。

4.2 如何得到分段模型

在已知上面部分内容的前提下，选取冰骗骗花为测试对象，提前测试出9.5s雷元素一下破其一半的冰甲，12s雷元素一下破完，即12s雷元素的破甲值为9.5s雷元素的两倍。正式测试中，在骗骗花给自己套上冰甲之前提前附着雷元素，此时与冰甲反应的是已经过衰减的元素。不难发现破甲值按一定规律随附着时间增加而减少。通过衰减破甲与满额破甲的比值算出衰减后对应的元素量，最终得出上面的9.5s与12s分段图像。

五、一些奇怪的补充

5.1 叠加情况为什么说只看时间不看元素量

为得出这个结论，需要在反应后残留的元素上进行同元素叠加，这里选用12s冰+弱岩结晶后叠加一9.5s冰。弱岩会消耗0.5的元素量，正常情况下12s冰会残留至约8.3s。一组测试数据为12s冰附着后，在1.03s施加岩触发结晶反应，紧接着在2.05s叠加一9.5s冰元素，最终冰元素在8.4s消失。

如果按元素量考虑，代入公式可得，2.05s叠加时被消耗后的12s元素只留有约0.82的元素量，小于9.5s元素补充的1的元素量。那么按元素量考虑，残留元素理应会被覆盖，从而总持续时间变为8.05s(按线性补充)或9.6s(按分段补充)。但实际情况仍然是8.4s为未受叠加元素影响的状态，符合按时间比较的2.05+6=8.05<8.4。

综合上述情况，才有了叠加只看时间判断是否覆盖的结论。

5.2 复杂情况下的衰减模型变化

如果反应前元素经过叠加而无法直接套用上述模型，只需将所有数据放缩至对应情况即可。例如9.5+12的叠加后，为得到对应的最大元素量为2而总时长为19s的模型，只需将12s模型数据的横坐标放大至19/12倍。猜测可能具有某一个类似单位图像的存在，每个情况计算时只需将单位图像放大至对应情况即可。

5.3 奇怪的现象

岩元素打冰结晶会先显示一帧雷和冰而后才变为岩和冰，其他反应也存在类似显示一帧错误元素图像的奇怪情况。